Appendix 2: Multilocus F-statistics
(as it appears in the DOS version 3.4 documentation written by Francois Rousset)
Fis may be defined as 
, where the QÕs are probability of identity in state of pairs of genes either within (Q1>) or between (Q2) individuals within subpopulations. Fst may likewise be defined as 
where Q3 is the probability of identity in state of pairs of genes between subpopulations. It can be estimated as 
where the 
Õs are frequencies of identical pairs of genes in the sample. These estimates may be expressed in terms of the mean sums of squares MSG, MSI, MSP computed by an analysis of variance:
, 
, and 
where nc is a function of the size of each sample.
With several loci, such an analysis is performed for each locus i. However, there is no single obvious way to compute multilocus F-statistics. Weir and Cockerham's (1984) multilocus estimators are defined from sums of intermediate statistics a, b, and c for each locus. The numerator of Fst of Weir and Cockerham (1984) is the sum over alleles of the a terms, 
. WeirÕs (1996) estimators are defined from sums of intermediate statistics S1, S2, and S3. The numerator of Weir (1996) is the sum over alleles of the S1 terms which are 
where
is an average over all loci. The 1984 and 1996 estimators slightly differ, but both give the same weight to the estimates of the 
Õs for a locus typed at 5 individuals in each subpopulation as for a locus typed at 50 individuals in each subpopulation..
Genepop uses yet other formulas. The multilocus estimator of Genepop has numerator 
, which will give 10 time more weight to the Q estimates for the more intensively typed locus. Explicit formulas for the estimators are (the estimators are sometimes expressed in terms of 
,
, and 
):
.
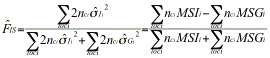
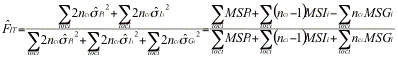
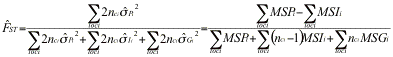The following example (due to A.J. Gharrett) illustrates the results obtained by the different methods for the data shown here.
| Estimate | Fis | Fst | Fit |
| Loc1 | -0.0483 | 0.5712 | 0.5505 |
| Loc2 | -0.1161 | 0.8560 | 0.8393 |
| Loc3 | 0.0051 | -0.0023 | 0.0028 |
| Multilocus (1984 a,b,c method) | -0.0286 | 0.5606 | 0.5480 |
| Multilocus (1996 S1,S2,S3 method) | -0.0286 | 0.5633 | 0.5508 |
| Multilocus (Genepop v3.3 and later) | -0.0275 | 0.5436 | 0.5310 |
Most of the time the different estimators yield close values.
Note that options 5.2 and 5.3 also return unweighted averages of MSG over loci.